本文运用上文中多维随机变量分布转换规律，来推导出PBRT中一系列重要结论

---

极坐标与笛卡尔坐标

已知$p(x, y)=\frac{p(r, \theta)}{\vert J_t(r, \theta) \vert}$，其中
$\begin{array}{c}{T}_1(r,\theta )=rcos\theta =x\\ T_2(r,\theta )=rsin\theta =y\end{array}$
\begin{array}{l}
T_1(r,\theta)=rcos\theta=x \\
T_2(r,\theta)=rsin\theta=y
\end{array}

$J_t(r, \theta)=\left[$
\begin{matrix}
cos\theta & -rsin\theta \\
sin\theta & rcos\theta \\
\end{matrix}
\right] = r

则有$p(r, \theta) = rp(x, y)$

---

球坐标与笛卡尔坐标

$\begin{array}{c}{T}_1(r,\theta ,\varphi )=rsin\theta cos\varphi =x\\ T_2(r,\theta ,\varphi )=rsin\theta sin\varphi =y\\ T_3(r,\theta ,\varphi )=rcos\theta =z\end{array}$
\begin{array}{l}
T_1(r,\theta, \phi)=rsin\theta cos\phi = x \\
T_2(r,\theta, \phi)=rsin\theta sin\phi = y \\
T_3(r,\theta, \phi)=rcos\theta = z
\end{array}

则$p(x, y, z)=\frac{p(r, \theta, \phi)}{\vert J_t(r, \theta, \phi) \vert}$，其中

$J_t(r, \theta, \phi)=\left[$
\begin{matrix}
sin\theta cos\phi & rcos\theta cos\phi & -rsin\theta sin\phi \\
sin\theta sin\phi & rcos\theta sin\phi & rsin\theta cos\phi \\
cos\theta & -rsin\theta & 0\\
\end{matrix}
\right] = r^2sin\theta

则有$p(r, \theta, \phi) = r^2sin\theta p(x, y, z)$。

---

立体角与球坐标

立体角的定义为在单位圆上投影的面积，在球坐标中有$d\omega=sin\theta d\theta d\phi$成立

因此基于物理Lambertion中的$\int_{\Omega}{f(\omega_i, \omega_o, p)cos\theta d\omega}$=1, 可得$f(\omega_i, \omega_o, p) = \frac{1}{\int_{0}^{2\pi}d\phi \int_{0}^{\frac{\pi}{2}}{cos\theta sin\theta d\theta}} = \frac{1}{\pi}$

若定义在某区域$\Omega$上的概率为$Pr\{ \omega \in \Omega \} = \int_{\Omega}{p(\omega)d\omega}$，也有$Pr\{ (\theta ,\phi) \in \Omega '\} = \int_{\Omega '}{p(\theta, \phi)d\theta d\phi}$

因此
$p(\theta, \phi)d\theta d\phi=p(\omega) d\omega$
$p(\theta, \phi)=sin\theta p(\omega)$

---

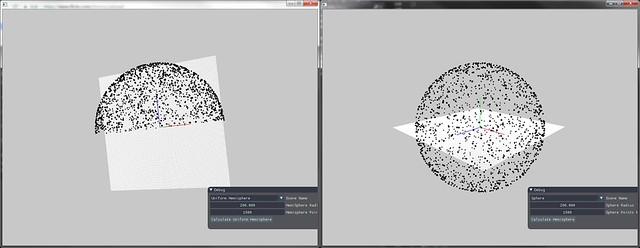
半球上立体角均匀采样

要对单位半球做关于立体角的均匀采样，则$p(\omega)=\frac{1}{2\pi}$，根据上文中与球坐标关系，$p(\theta, \phi)=\frac{sin\theta}{2\pi}$。

则有两独立同均匀分布随机变量$(\xi,\psi)\in [0,1]$，要转换成满足半球上均匀分布的球坐标表示。

$p(\theta) = \int_{0}^{\frac{\pi}{2}}p(\theta, \phi)d\phi = sin\theta, \quad p(\phi) = \int_{0}^{2\pi}p(\theta, \phi)d\theta = \frac{1}{2\pi}$

$p(\theta \vert \phi) = \frac{p(\theta, \phi)}{p(\phi)}=sin\theta, \quad p(\phi \vert \theta) = \frac{p(\theta, \phi)}{p(\theta)}=\frac{1}{2\pi}$

这里很明显可以看出来$\theta,\phi$为两个独立随机变量

$Pr\{\theta' \leqslant \theta\} = \int_{0}^{\theta}p(\theta)d\theta=1-cos\theta , Pr\{\phi' \leqslant \phi\} = \int_{0}^{\phi}p(\phi)d\phi=2\pi \phi$

应用反CDF变换法则，$P^{-1}(\theta)=1-arccos\theta, P^{-1}(\phi)=2\pi \phi$，因此
$\begin{array}{c}\theta =arccos(1-\xi )=arccos\xi \\ \varphi =2\pi \psi \end{array}$
\begin{array}{l}
\theta=arccos(1-\xi)=arccos\xi \\
\phi=2\pi \psi
\end{array}

由于球坐标不容易在计算机中表示，因此转换为笛卡尔表示

$\begin{array}{c}x=sin\theta cos\varphi =\sqrt{1-{\xi }^2}cos2\pi \psi \\ y=sin\theta sin\varphi =\sqrt{1-{\xi }^2}sin2\pi \psi \\ z=cos\theta =\xi \end{array}$
\begin{array}{l}
x=sin\theta cos\phi=\sqrt{1-\xi^2}cos2\pi \psi \\
y = sin\theta sin\phi = \sqrt{1-\xi^2}sin2\pi \psi \\
z = cos\theta = \xi
\end{array}

同理可推证球上立体角均匀采样

$\begin{array}{c}x=2\sqrt{\xi (1-\xi )}cos2\pi \psi \\ y=2\sqrt{\xi (1-\xi )}sin2\pi \psi \\ z=1-2\xi \end{array}$
\begin{array}{l}
x=2\sqrt{\xi(1-\xi)}cos2\pi \psi \\
y = 2\sqrt{\xi(1-\xi)}sin2\pi \psi \\
z = 1-2\xi
\end{array}

下图为半球上均匀采样的结果与完整球上均匀采样的结果

---

单位圆上的均匀采样

要根据面积对单位圆上进行均匀采样，$p(x,y)=\frac{1}{\pi}$，则$p(r, \theta)=rp(x,y)$。

$p(\theta)=\int_{0}^{1}\frac{r}{\pi}dr=\frac{1}{2\pi}, \quad p(r\vert \theta)=\frac{p(r,\theta)}{p(\theta)}=2r$

则他们对于的CDF为$P(\theta)=\int_{0}^{\theta}p(\theta)d\theta=\frac{\theta}{2\pi}$，$P(r\vert \theta)=\int_{0}^{r}p(r\vert \theta)dr=r^2$

求出其对应反函数$P^{-1}(\theta)=2\pi\theta$，$P^{-1}(r\vert \theta)=\sqrt{r}$

若有两满足在$[0, 1]$上均匀分布的随机变量$\xi, \psi$有$\theta=2\pi \xi, r=\sqrt{\psi}$

则转换回笛卡尔坐标结果为

$\begin{array}{l}$
x = \sqrt{\psi}cos2\pi \xi\\
y = \sqrt{\psi}sin2\pi \xi
\end{array}

这里$r, \theta$也是两个独立的随机变量

PBRT中论述的Concentric Disk Sampling可以参见前文Depth of Field中的实现与可视化

---

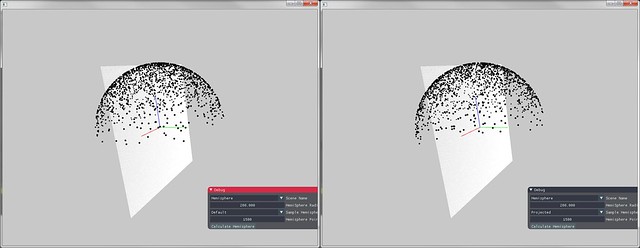
基于Cosine函数的半球采样

这里使用基本的转换思路，$p(\omega)\propto cos\theta$，因此$p(\omega)=\frac{cos\theta}{\pi}$

有$p(\theta, \phi)=\frac{sin\theta cos\theta}{\pi}$，则有

$p(\theta)=\int_{0}^{2\pi}p(\theta, \phi)d\phi=2sin\theta cos\theta, \quad p(\phi \vert \theta)=\frac{p(\theta, \phi)}{p(\theta)}=\frac{1}{2\pi}$

可得CDF为

$P(\theta)=\int_{0}^{\theta}p(\theta)d\theta=\frac{1-cos2\theta}{2}, \quad P(\phi \vert \theta)=\int_{0}^{\phi}p(\phi \vert \theta)d\phi=\frac{\phi}{2\pi}$

应用反CDF得$P^{-1}(\theta)=\frac{1}{2}arccos(1-2\theta), P^{-1}(\phi \vert \theta)=2\pi \phi$

$\begin{array}{c}\theta =\frac{1}{2}arccos(1-2\xi )\\ \varphi =2\pi \psi \end{array}$
\begin{array}{l}
\theta = \frac{1}{2}arccos(1-2\xi)\\
\phi = 2\pi \psi
\end{array}

转换为笛卡尔下的表示为
$\begin{array}{l}$
x=sin\theta cos\phi = sin(\frac{1}{2}arccos(1-2\xi)))cos2\pi\psi \\
y=sin\theta sin\phi = sin(\frac{1}{2}arccos(1-2\xi)))sin2\pi\psi\
z=cos\theta = cos(\frac{1}{2}arccos(1-2\xi))
\end{array}

PBRT中给出了另一种计算办法，将均匀分布在圆盘上的点投影到半球上，其结果就满足Cosine-Weighted。

以下给出证明

假定在圆盘上的极坐标分布为$p(r, \phi)=\frac{r}{\pi}$（使用$\phi$方便后续将$r$对应为$\theta$相关），$p(r, \phi)=\frac{p(\theta, \phi)}{\vert J_t(r, \theta)\vert}$

$\begin{array}{c}r=sin\theta =T_1\left(r\right)\\ \varphi =\varphi =T_2\left(\varphi \right)\end{array}$
\begin{array}{l}
r=sin\theta = T_1(r) \\
\phi=\phi = T_2(\phi)
\end{array}

$J_t(r, \theta)=\left[$
\begin{matrix}
cos\theta & 0 \\
0 & 1 \\
\end{matrix}
\right] = cos\theta

即有$p(\theta, \phi)=cos\theta p(r, \phi)=\frac{r cos\theta}{\pi} = \frac{sin\theta cos\theta}{\pi}$，和上述中得到的结果一样。

下图为两种方法产生的Cosine-Weighted对比

---

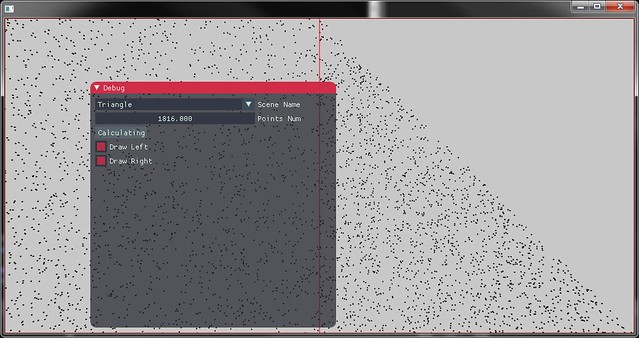
三角形均匀采样

PBRT中采用了等腰切两边为1的三角形特殊情况，不过以下计算办法可以变换回任何三角形

有$p(u,v)=2$（面积倒数），则有

$\begin{array}{c}p\left(u\right)={\int }_0^{1-u}p(u,v)dv=2-2u,p\left(v\mathrm{\mid }u\right)=\frac{p(u,v)}{p\left(u\right)}=\frac{1}{1-u}\\ P\left(u\right)={\int }_0^{u}p\left(u\right)du=2u-u^2,P\left(v\mathrm{\mid }u\right)={\int }_0^{v}p\left(v\mathrm{\mid }u\right)dv=\frac{v}{1-u}\end{array}$
\begin{array}{l}
p(u)=\int_{0}^{1-u}p(u,v)dv=2-2u, \quad p(v\vert u)=\frac{p(u,v)}{p(u)}=\frac{1}{1-u} \\
P(u)=\int_{0}^{u}p(u)du=2u-u^2, \quad P(v\vert u)=\int_{0}^{v}p(v\vert u)dv=\frac{v}{1-u}
\end{array}

这里反变换CDF开根号时要注意到$u,v\in [0,1]$

因此有$u=1-\sqrt{\xi},v=\sqrt{\xi}\psi$

下图中即为三角形上的均匀采样

---

根据二维分段函数分布采样

这里分段函数的采样即为离散随机变量，若有横向纵向各$n_u,n_v$个元素，函数上指定位置一点值为$f(u,v)$，那么就有

$\begin{array}{c}{I}_f={\int }_v{\int }_{u}f(u,v)dudv=\frac{1}{n_u{n}_v}{\sum }_{i=0}^{n_u-1}{\sum }_{j=0}^{n_v-1}f(u_i,v_j)\\ p(u,v)=\frac{f(u,v)}{I_f}\end{array}$
\begin{array}{c}
I_f=\int_v \int_u f(u,v)dudv=\frac{1}{n_un_v}\sum_{i=0}^{n_u-1}\sum_{j=0}^{n_v-1}f(u_i,v_j) \\
p(u,v)=\frac{f(u,v)}{I_f}
\end{array}

而边缘概率密度可直接得到
$p(u)=\int_v p(u,v)dv=\frac{\frac{1}{n_u}\sum_i f(u, v_i)}{I_f} , \quad p(v\vert u)=\frac{p(u,v)}{p(u)}=\frac{f(u,v)}{\frac{1}{n_u}\sum_i f(u, v_i)}$

之后利用CDF反变换，即PBRT中distribution1d的实现办法可完成对于$p(u),p(v\vert u)$上的采样

此处效果可见前文中的二维分段函数采样的结果

---

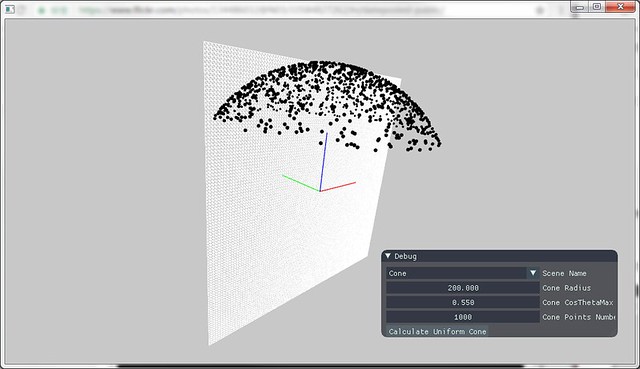
圆锥均匀采样

类似于球上的均匀采样, 易证随机变量$\theta, \phi$相互独立

已知$p(\omega)=\frac{1}{2\pi(1-cos\theta_{max})}$，则$p(\theta, \phi)=\frac{sin\theta}{2\pi(1-cos\theta_{max})}$

$p(\theta)=\int_{0}^{2\pi}p(\theta, \phi)d\phi=\frac{sin\theta}{1-cos\theta_{max}}, \quad p(\phi)=\int_{0}^{2\pi}\frac{sin\theta}{2\pi(1-cos\theta_{max})}d\theta=\frac{1}{2\pi}$

$P(\theta)=\int_{0}^{\theta}\frac{sin\theta}{1-cos\theta_{max}}d\theta=\frac{1-cos\theta}{1-cos\theta_{max}}, \quad P(\phi)=\int_{0}^{\phi}\frac{1}{2\pi}d\phi=\frac{\phi}{2\pi}$

若有两随机变量$xi, \psi$，运用反变换可有（此处省略了$\theta, \phi$到笛卡尔的转换）

$cos\theta=1-\xi +\xi cos\theta_{max}, \quad \phi=2\pi\psi$

下图中即为圆锥上的均匀采样